Lab Report

Individual Report
Due date: 8 April 2025 (Tuesday), 23:59
Include: Code, figures, and anything you think it is important :)
If you have any questions, please contact me by email: ningg.han@connect.polyu.hk (Han Ning)

---

Question 1 (25 Pts.)

The open-loop zero-pole distribution diagram of a system is as follows, ○ represents zero and X denotes pole. Try to roughly draw the corresponding root locus. (Hint: Estimate the values of zero and pole with your eyes).

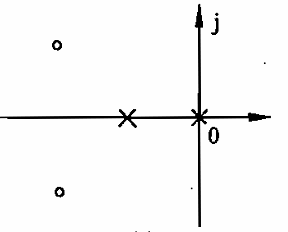
Question 2 (25 Pts.)

For the following system,
a) compute the total transfer function (using the commands studied in the tutorial) for the following 3 cases: \( G_c(s) = s \), \( G_c(s) = s^2 \), \( G_c(s) = \frac{s^2}{s+20} \).
b) Draw the root locus for each of these 3 cases.

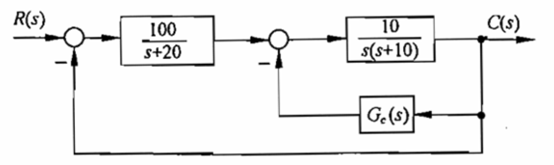
Question 3 (25 Pts.)

Simulate the system in the following picture and try different values of PID parameters and decide the best group of parameters, then plot the response curve of the system.

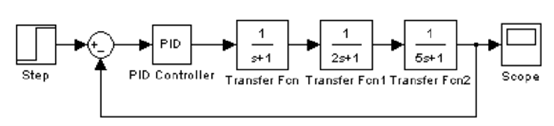
Question 4 (25 Pts.)

This is the definition of Fibonacci numbers. Please write a function which can calculate the nth Fibonacci number according to the definition and test it with n = 3, 9 and 15. The shorter your code is, the more score you will obtain. (Only the methods mentioned in the class are allowed to be used).