Advanced Matlab/Octave Tutorial

Usage in Octave

To use the functions "series", "parallel", "feedback" in Octave, you may need to load the control package firstly. You can add the following script to the beginning of your code to solve it.

                            pkg load control;

Transfer Functions

To build a control system, the first step is to build the system model. In general, we can use transfer functions represent the system model. Matlab offers powerful tools for representing the system model. Next, let's study how to depict the transfer functions in Matlab.

In Matlab, the function to create the transfer function models is "tf". In general, you can use two types of syntax to create the transfer function. The first one is

                                s = tf('s');
                                sys = transfunc

For example, create a new file and type the following scripts in it,

                                s = tf('s')
                                sys = 4/(s^3+2*s^2+3*s+4)

If you run the script, you will see the following result in the command window.

The second type of syntax is

                                num = [numerators];
                                den = [denominators];
                                sys = tf(num, den)

For example, create a new file and type the following scripts in it,

                                num = [1, -3];
                                den = [1, 3];
                                sys = tf(num, den)

If you run the script, you will see the following result in the command window.

Partial Fraction Decomposition

In many cases, we need to use the partial fraction decomposition of the transfer functions. However, it could be very difficult to find the partial fraction decomposition of a transfer function with high order and complex structures. In Matlab, it offers a simple function to solve the problem.

The syntax for computing the partial fraction decomposition of transfer functions is

                                num = [numerators];
                                den = [denominators];
                                [r, p, k] = residue(num, den)

where, "r", "p", "k" are vectors containing the residues, poles and direct terms, respectively.

Let's see an example. Compute the partial fraction decomposition of the following transfer function.

$$\frac{B(s)}{A(s)}=\frac{2s^3+5s^2+3s+6}{s^3+6s^2+11s+6}$$
create a new file and type the following scripts in it,

                                num = [2, 5, 3, 6];
                                den = [1, 6, 11, 6];
                                [r, p, k] = residue(num, den)

If you run the script, you will see the following result in the command window.

So, now we can write the partial fraction decomposition of the transfer function as

$$\frac{B(s)}{A(s)}=\frac{-6}{s+3}+\frac{-4}{s+2}+\frac{3}{s+1}+2$$
The function "residue" can also convert the "[r, p, k]" into numerators and denominators. For example, using the result we got in the previous example, create a new file and type the following scripts in it,

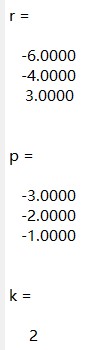
                                r = [-6, -4, 3];
                                p = [-3, -2, -1];
                                k = 2;
                                [num, den] = residue(r, p, k)
                                sys = tf(num, den)

If you run the script, you will see the following results in the command window.

Arithmetic of Transfer Function

The arithmetic of transfer function in Matlab is similar to scalars and vectors. You can use the following syntax to compute the addition, subtraction, multiplication, inverse and division of systems.

                                sys = sys1 + sys2
                                sys = sys1 - sys2
                                sys = sys1*sys2
                                sys = inv(sys1)
                                sys = sys1\sys2 (equals to inv(sys1)*sys2)
                                sys = sys1/sys2 (equals to sys1*inv(sy2))

Connection of System Models

In general, a system has different structures, such as series connection, parallel connection, and feedbacks. Matlab also provides powerful tools to connect different parts of the system.

The series connection of two sub-systems can be created by the following syntax

                                sys = series(sys2, sys1)

The function "series" implements the following operation

The parallel connection of two sub-systems can be created by the following syntax

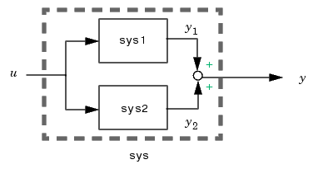
                                sys = parallel(sys1, sys2)

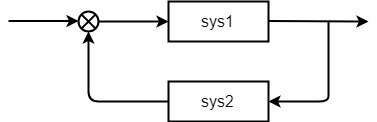
The function "parallel" implements the following operation

The feedbacks can be created by the following syntax

                                sys = feedback(sys1, sys2, sign)

The function "feedback" implements the following operation. If "sign=1", it gives a positive feedback. If "sign=-1", which is the default value, it gives a negative feedback.

Now, let's see an example. Compute the transfer function of the following system.

Create a new file and type the following scripts in it,

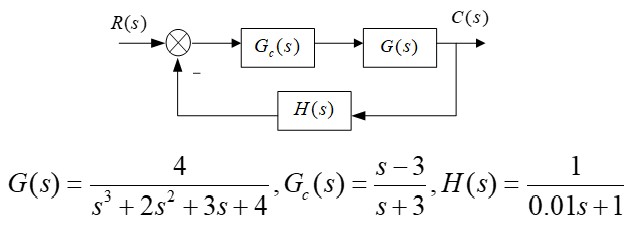
                                s = tf('s');
                                G = 4/(s^3+2*s^2+3*s+4);
                                G_c = (s-3)/(s+3);
                                H = 1/(0.01*s+1);

                                sys1 = series(G, G_c);
                                sys = feedback(sys1, H)

If you run the script, you will see the following result in the command window.