Advanced Matlab/Octave Tutorial -- System Analysis


Usage in Octave

To use the functions "step", "impulse", "lsim", "pole", and "pzmap" in Octave, you may need to load the control package firstly. You can add the following script to the beginning of your code to solve it. 
                            pkg load control;

Time Responses

The time response represents how the state of a dynamic system changes in time when subjected to a particular input, such as step response, impulse response and initial condition response. For some systems, we can analytically find a closed-form solution. However, for most systems, the closed-form analytical solutions are hard to find, which brings difficulties to the analysis of their time responses. Fortunately, Matlab provides powerful tools for analyzing the time responses of dynamic systems.

Step Response
The step response of dynamic system is calculated by function "step" in Matlab. The syntax is as follows: 
                                t = 0:dT:T;
                                step(sys, t);
where "dT" is the time step for simulation, "T" is the stop time of the simulation, and "sys" is the transfer function. Note that "t" is an optional argument. If you have the numerators and denominators of the transfer function, you can also use the following script to get the step response. 
                                t = 0:dT:T;
                                step(num, den, t);
After you run the script, a figure with the step response will be shown to you. Sometimes, we want to save the simulation data for further analysis, then the following syntax can be used. 
                                t = 0:dT:T;
                                [y, t] = step(sys, t); or [y, t] = step(num, den, t);
                                plot(t, y);
In this case, the response data of the dynamic system will be saved to vector "y", but there will not be a figure showing the step response. Therefore, we need to call the "plot" function to draw the step response. With data "y" and "t", we can calculate the rise time, peak time, maximum overshoot, and settling time of the step response. The syntax is 
                                stepinfo(y, t); or stepinfo(sys);
The function will return a structure containing the information of the step response. Note that this function is not available in Octave.

Let's see an example. Calculate the step response of the following system.

$$G(s)=\frac{1}{s^2+0.6s+1}$$
Create a new file and type the following script in it. 
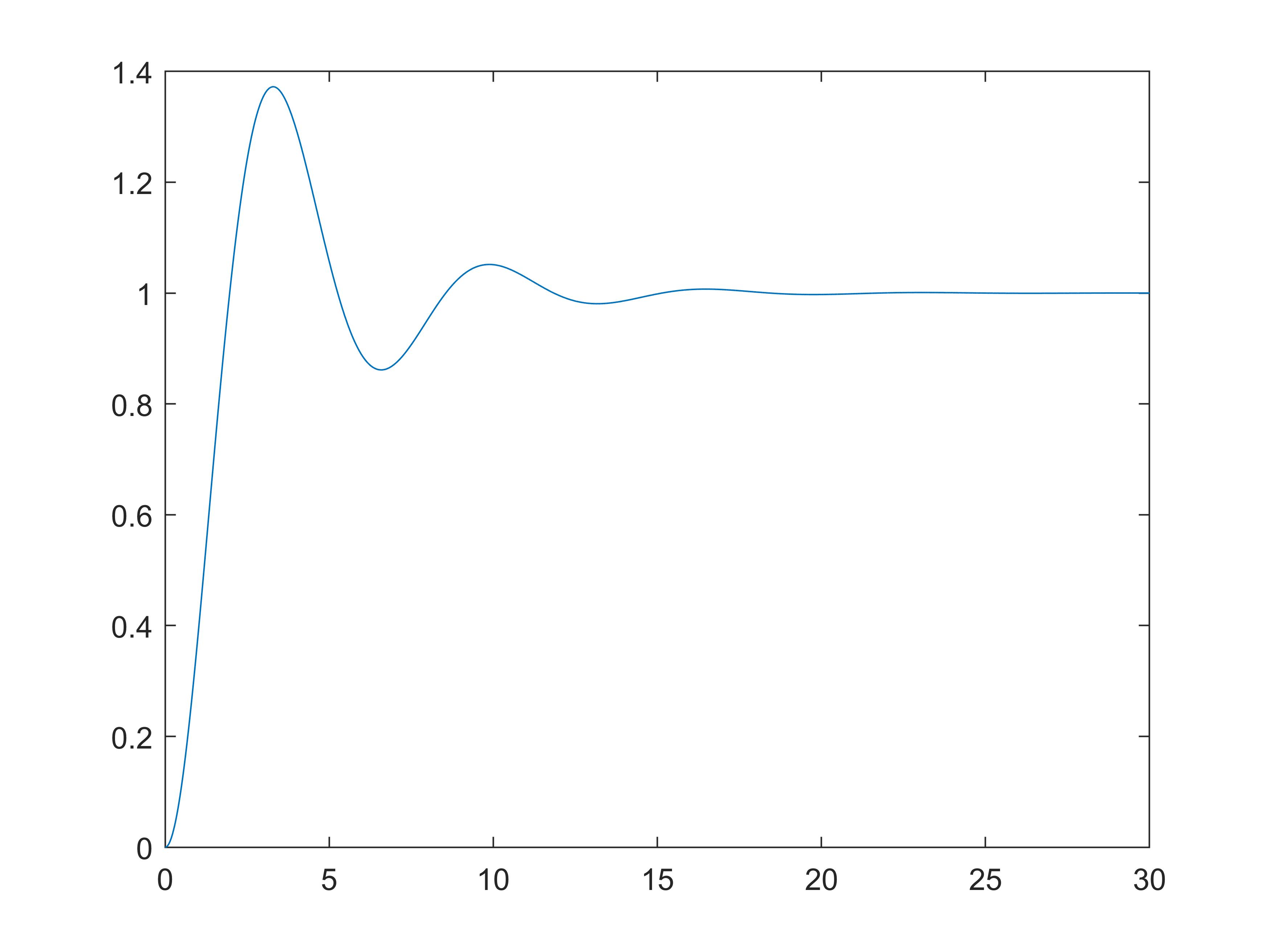
                                s = tf('s');
                                sys = 1/(s^2+0.6*s+1);

                                t = 0:0.001:30;
                                [y, t] = step(sys, t);
                                plot(t, y);
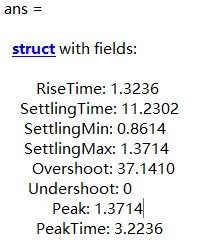
                                stepinfo(y, t)
Run the file, and you can get the figure and the step response information in the command window.
Impulse Response
The impulse response of dynamic system is calculated by function "impulse" in Matlab. The syntax is similar to that of step response: 
                                t = 0:dt:T;
                                [y, t] = impulse(sys, t); or [y, t] = impulse(num, den, t);
                                plot(t, y);
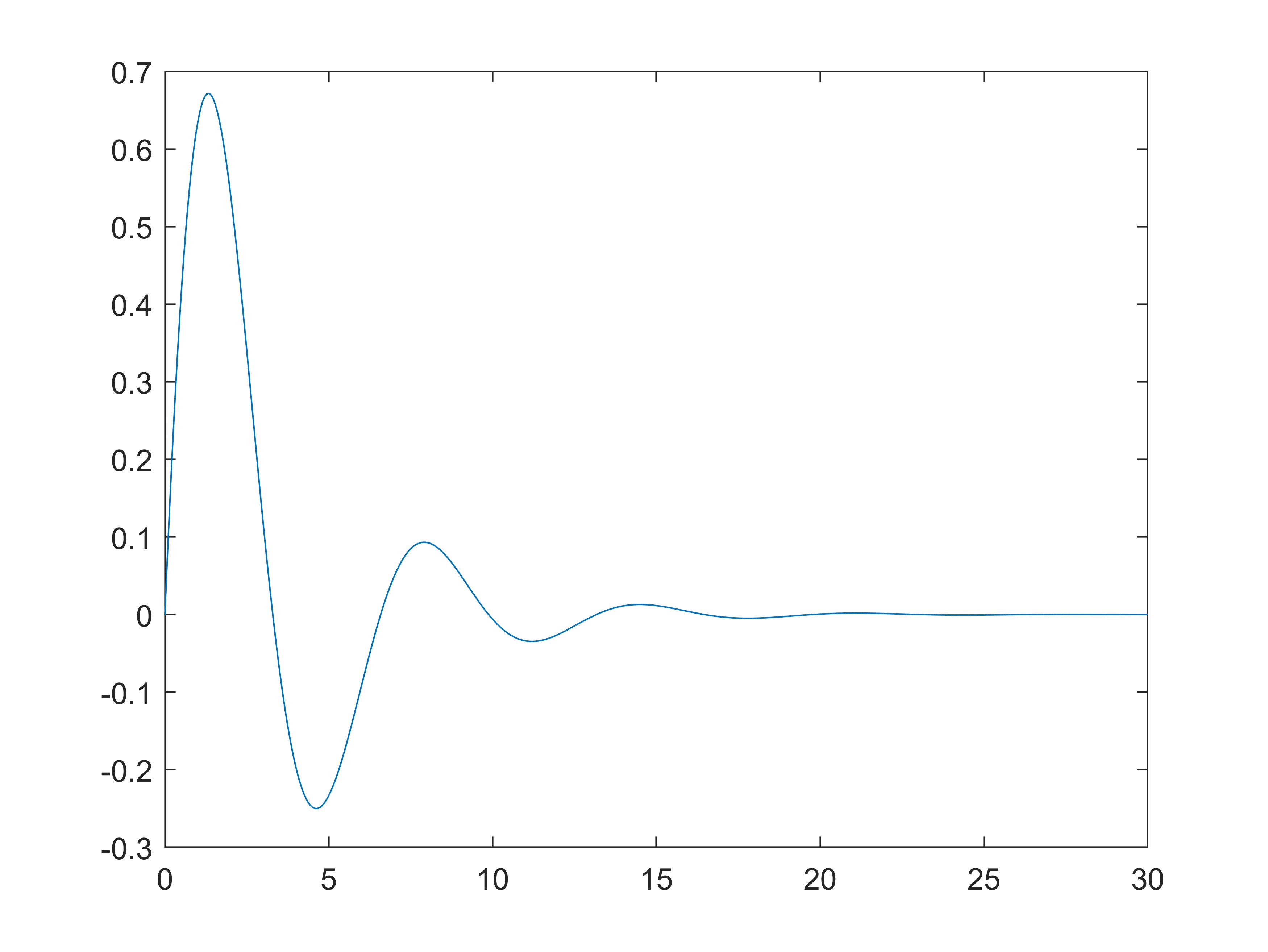
Let's use the previous example to see the impulse response.Create a new file and type the following script in it. 
                                s = tf('s');
                                sys = 1/(s^2+0.6*s+1);

                                t = 0:0.001:30;
                                [y, t] = impulse(sys, t);
                                plot(t, y);
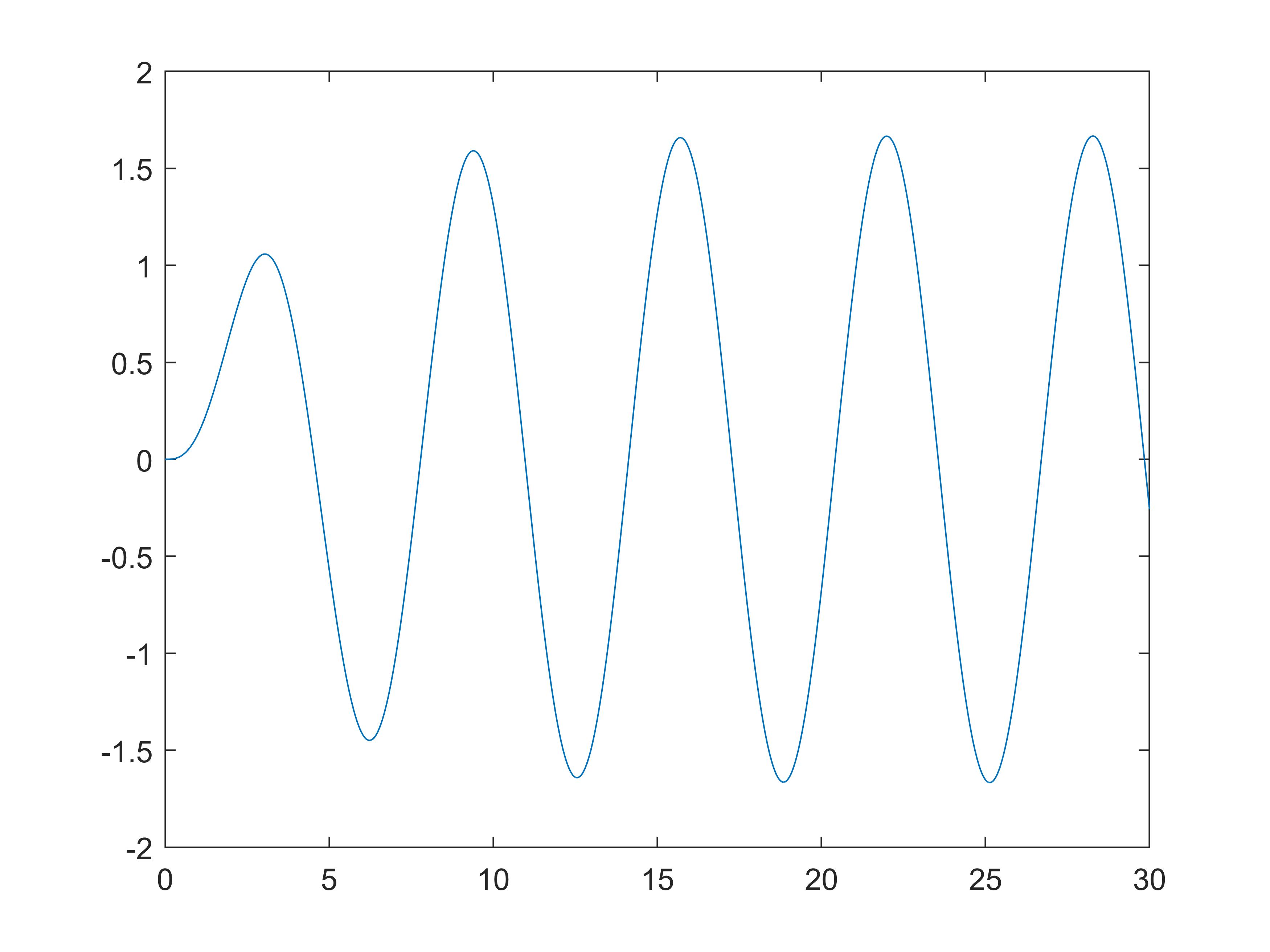
Run the file, and you can get the figure showing the impulse response.
Arbitrary Input Response
The arbitrary input response of dynamic system is calculated by function "lsim" in Matlab. The syntax is as following 
                                t = 0:dt:T;
                                [y, t] = lsim(sys, u, t); or [y, t] = lsim(num, den, u, t);
                                plot(t, y);
where "u" is the predefined input.

Let's use the previous example again to see the time response with a sin input signal.Create a new file and type the following script in it. 
                                s = tf('s');
                                sys = 1/(s^2+0.6*s+1);

                                t = 0:0.001:30;
                                [y, t] = lsim(sys, sin(t), t);
                                plot(t, y);
Run the file, and you can get the figure showing the impulse response.

Stability Analysis

As we all know, stability analysis of the dynamic systems is one of the most important problems in linear systems and control. There are many ways to analyze the stability. Matlab provides great tools for stability analysis.

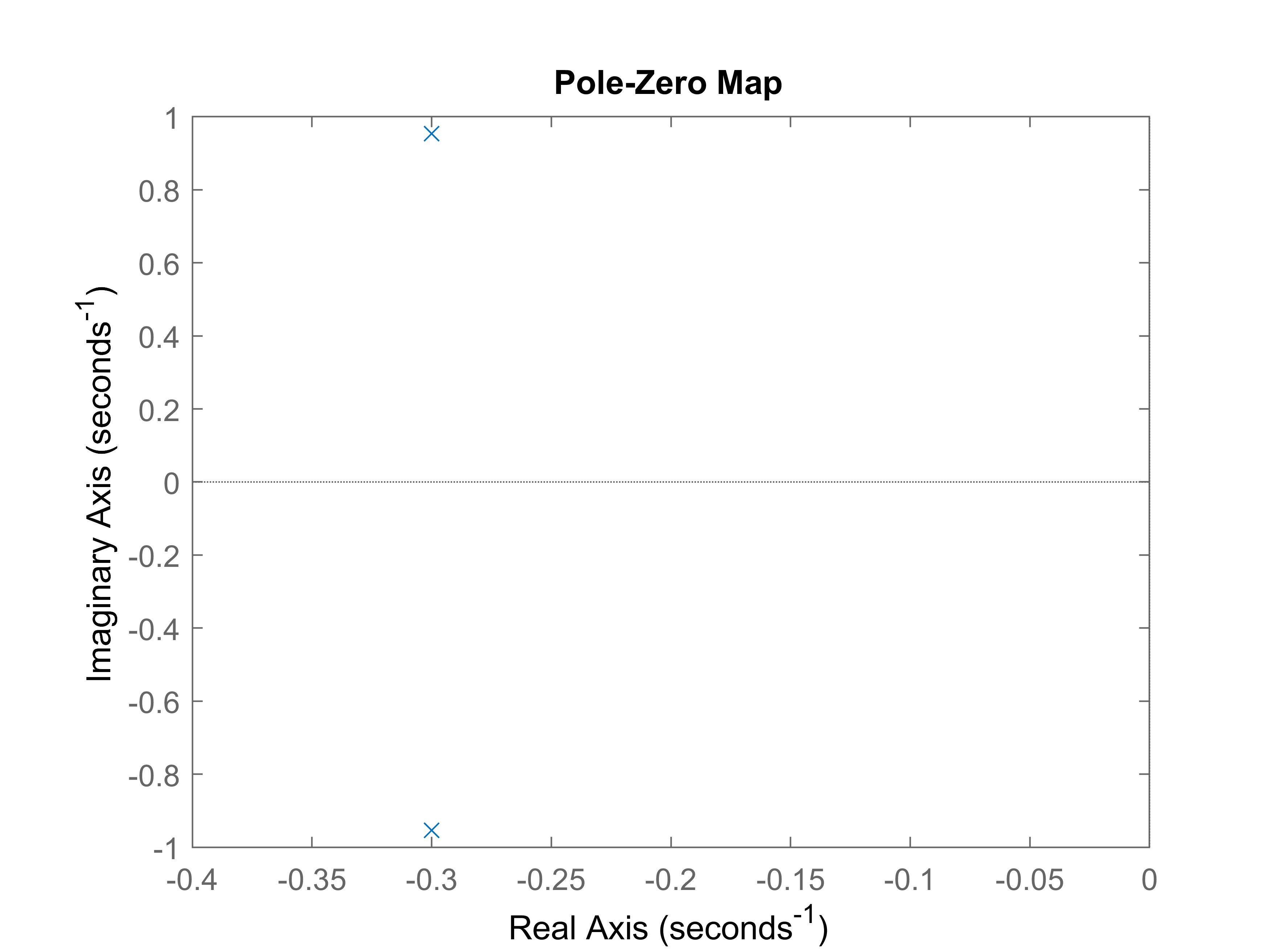
Stability Analysis Based on Poles' locations
One intuitive way to analyze the stability of systems is to calculate the poles and make the analysis based on their locations. Basically, there are two methods to calculate the poles in Matlab.

The first method is to use the function "roots". The syntax is as following 
                                den = [denominators];
                                roots(den)
To use this method, we only need to know the denominators of the transfer functions.

Let's use the previous example to do the stability analysis. Type the following script in the command window 
                                den = [1, 0.6, 1];
                                roots(den)
Run the script, and you will see the following results in the command window.
If we have the complete transfer function of the system, we can also use the second method. The Syntax is as following: 
                                s = tf('s');
                                G = transFunc;
                                pole(G)
Also, we can use the following script to show the poles and zeros in a pole-zero map. 
                                pzmap(G);
Let's use the previous example again to analyze the stability with the second method. Create a new file and type the following script in it. 
                                s = tf('s');
                                G = 1/(s^2+0.6*s+1);
                                pole(G)
                                pzmap(G);
                                axis([-0.4, 0, -1, 1]);
Run the file and you will see the pole-zero map and the poles in the command window.
As you can see, the results from both methods are exactly the same.

In addition, the Matlab/Octave also offer a tool to get the root locus of the system. You can achieve that by simply calling the following functon 
                                rlocus(sys);
For the system in previous example, create a new file and type the following script in it 
                                s = tf('s');
                                G = 1/(s^2+0.6*s+1);
                                rlocus(G);
Run the file, then we can get



Back to Top